1. Le formalisme de l’apprentissage automatique
L’apprentissage automatique est la science regroupant les algorithmes ayant la capacité d’apprendre des données. Cette notion d’apprentissage est représentée mathématiquement de la façon suivante:

Ici, x représente un ensemble de données. Pour chaque donnée x_i (un scalaire, un vecteur, une matrice ou un tenseur), il existe une valeur associée y_i à apprendre. L’apprentissage automatique avec la fonction f revient à trouver ses paramètres w tels que le résultat ŷ_i estimé par la fonction soit le plus proche possible de la vérité y_i pour l’ensemble des x possibles.
Par exemple, si f est une fonction linéaire simple, on a w = [a,b] et donc f_[a,b](x_i) = a*x_i+b = ŷ_i. Il existe de nombreuses fonctions d’apprentissage automatique.
2. L’apprentissage des réseaux de neurones
Les réseaux de neurones font partis des algorithmes d’apprentissage profond qui sont une sous-catégorie des algorithmes d’apprentissage automatique. Un réseau de neurones est donc une fonction d’apprentissage automatique.
Pour apprendre des données, les réseaux de neurones effectuent une prédiction à partir de leur structure interne. Cette prédiction (qui a également la forme d’un scalaire, vecteur, d’une matrice ou d’un tenseur) dépend des paramètres (poids) du réseau, et de la donnée d’entrée.
Le réseau de neurones compare ensuite cette prédiction/estimation ŷ_i avec la vraie valeur à prédire y_i. En effectuant la différence, il connait son erreur. En apprentissage profond, l’ensemble des calculs permettant de calculer cette erreur sont différentiables, cela permet de calculer le gradient (la dérivée en un point) de sorte à modifier les paramètres w du réseaux dans la direction qui abaisse l’erreur.
Pour faire simple, le réseau voit des données, il fait une prédiction, il regarde son erreur et on a un algorithme pour le modifier et corriger cette erreur.
3. Une visualisation en pratique
Code utilisé: https://github.com/Whiax/NeuralDatavizTF
Pour faire de l’apprentissage, il nous faut une tâche. La voici:

La tâche est d’apprendre la couleur à donner à une croix à partir de sa position (a,b). On a donc x_i = [a,b] et y_i = [0] ou [1], avec 0 le jaune et 1 le bleu.
Le réseau de neurones est composé de deux couches cachées. Les données (un vecteur de dimension 2 pour a et b) sont en entrée, puis passent par un perceptron à 100 neurones (100 fonctions linéaires), puis par une fonction non-linéaire ReLU, c’est la première couche cachée, nous avons un vecteur de dimension 100 en sortie.
La 2ème est identique mais n’est composée que de 2 neurones, on a donc un vecteur de dimension 2 en sortie.
Enfin, le réseau prédit sa sortie avec la couche de sortie (un scalaire entre 0 et 1), qui sera remis à 0 ou à 1 avec un arrondi. Si le réseau prédit au dessus de 0.5, ŷ_i = 1, sinon ŷ_i = 0.
Si la prédiction est à 0.6 et que la vérité est à 1, le réseau doit se corriger de 0.4. Dans les faits, ce processus est incrémental, le réseau se corrigera d’une fraction de 0.4, par exemple de 0.01 * 0.4 = 0.004. On appelle alors ce facteur 0.01 le learning rate. Le réseau considère qu’il doit se corriger de 0.004 sur un paramètre et ajustera ses poids plus progressivement. Il effectue alors une itération. Un réseau nécessite de nombreuses itérations pour finir un entrainement.
Voici comment évolue le pourcentage de bonnes prédictions en fonction des itérations:

On voit que le réseau passe de 36% de bonnes prédictions à 82%. L’apprentissage fonctionne. Mais que s’est-t-il passé?
Les visuels
Et bien le réseau a modifié ses poids à partir de son erreur. Les détails de ces opérations sont expliqués à plusieurs endroits, mais peu de visuels existent.
En modifiant ses poids, le réseau modifie la représentation interne qu’il a des données. Ainsi, dans notre réseau de neurone, l’algorithme passe de la représentation initiale en entrée de dimension [2], à un vecteur de dimension [100], puis un autre de dimension [2] puis à sa sortie en dimension [1].
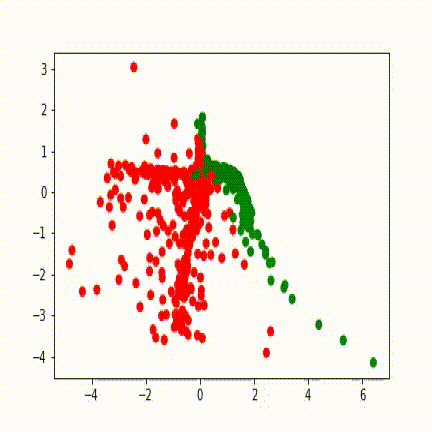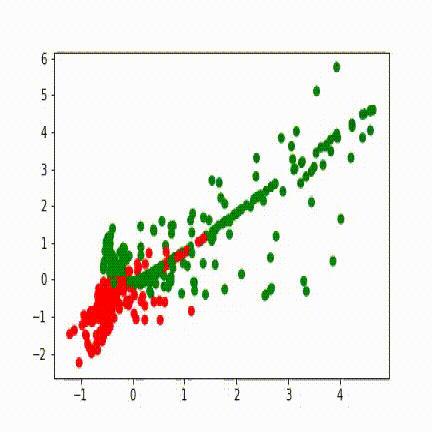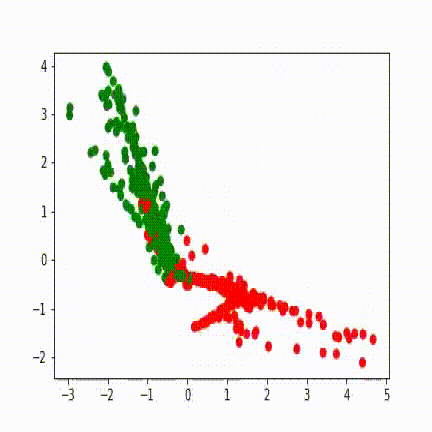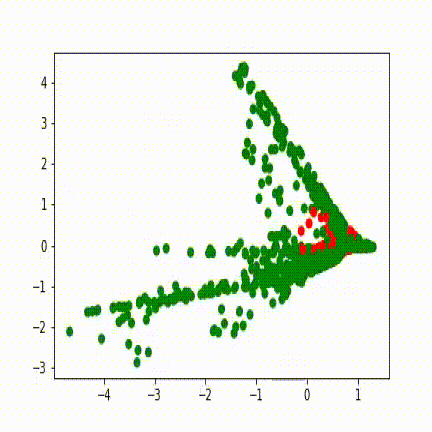
Voici des visuels, pour 3 entraînements différents, de l’évolution de l’avant dernière représentation, en fonction des itérations:
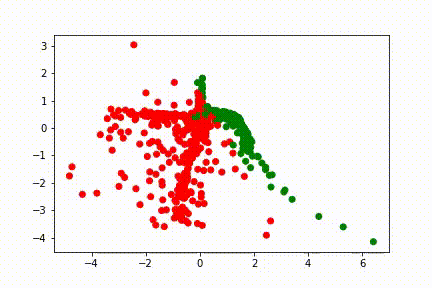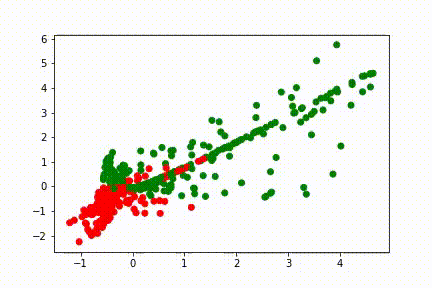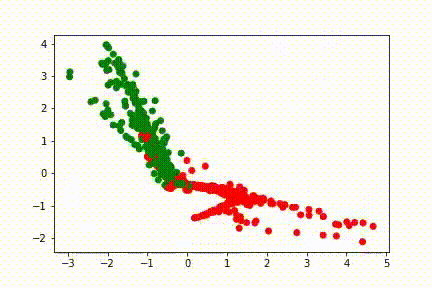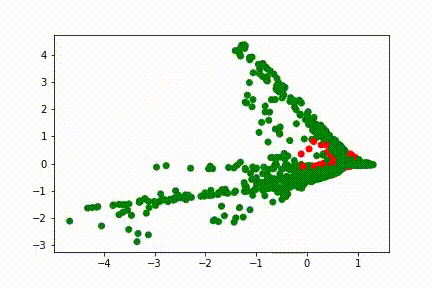
Sur ces visuels, chaque point correspond à une donnée d’entrée. Si le réseau de neurones était une fonction identité, nous retomberions sur des points aux positions de ceux de la tâche. Un point vert est une bonne classification, un point rouge est mal classifié.
Durant son apprentissage, le réseau de neurones a besoin de voir ces points autrement afin de pouvoir les classifier. La dernière fonction d’un réseau de neurones étant généralement simple, la complexité de création de cette représentation interne réside dans les couches qui précèdent. Ici, la couche de 100 neurones contient toute la complexité, et la couche de 2 neurones qui la suit sert à visualiser cette complexité. Les différentes lignes droites qui apparaissent représentent les droites partant de (0,0) et allant dans les coins de la tâche (5,5), (5,-5), (-5,5), (-5,-5).
Le réseau isole d’abord la zone (0,0) contenant le premier groupement de point de la classe bleue, puis essaie d’isoler la zone (3,3) qui contient le second groupement.
Les réseaux de neurones opèrent de façon cachée. Puisque leur erreur dépend de centaines de paramètres, il n’est pas possible de dire pourquoi ils progressent d’une façon plutôt que d’une autre sans faire une analyse longue, complexe et peu utile car elle n’est valide que pour une seule itération d’un seul entrainement donné. Ainsi il n’est pas possible d’aller plus loin dans le détail de l’évolution des visuels donnés sans faire de suppositions générales sur l’ensemble de ces paramètres.
Ici, l’idée est que le réseau de neurones cherche à transformer la représentation initiale en une représentation facile à traiter pour sa couche finale, c’est à dire une représentation qui permette de donner une forte valeur (proche de 1) à une des couleurs et une faible valeur à l’autre. L’idéal est donc de mettre les points bleus à un bout d’une droite ou d’un plan, et les points oranges à un autre bout.
C’est ce que nous pouvons imaginer voir sur ce dernier visuel qui cette fois utilise les couleurs de la tâche d’origine:

Les deux groupements de points bleus sont progressivement isolés par le réseau durant son apprentissage.
Conclusion
L’objectif de cette étude était d’analyser visuellement un apprentissage automatique. Ici, la tâche était très aisée, les données d’entrée n’était qu’en deux dimensions.
Si nous devons traiter des images de dimensions 1000*1000*3, la dimension d’entrée est alors de 3 millions. Si d’autant plus nous avons non pas deux mais 1000 classes à l’arrivée, il est illusoire de vouloir représenter efficacement cette complexité.
Néanmoins, le principe général demeure, les algorithmes d’apprentissage profond sont des algorithmes avec une forte capacité de représentation interne. Cette caractéristique fait partie de celles qui ont fait d’eux les fers de lance de la nouvelle génération d’algorithmes d’intelligence artificielle depuis les années 2010.
C’est cette capacité à internaliser une forte complexité qui les a rendu si puissants: il n’y a pas besoin de les diriger ni de les comprendre en profondeur pour qu’ils fonctionnent.
____________________________________________
Cet article a été rédigé dans le cadre d’une étude réalisée par et pour https://www.hyugen.com
Twitter: https://twitter.com/HyugenAI
